Hola todos!

I’m writing to you as Easter is coming to an end and world pandemic is still here, but the good news is, that here we are again. After a couple of discrete distributions, that were rather understandable I hope, today I would like to focus on the probability of an event occurrence in the given time/period. So let me start with…

Poisson distribution

Poisson distribution responds to a question: what is the probability of an occurrence of some number of events in a unit of time. (1)

But first, I haven’t covered it in my previous post or maybe it wasn’t clear enough, but the easiest probability distribution and the most basic one is a two-point distribution (that is what it is called in Polish, in English it is Bernoulli distribution, and (!) binomial distribution in Polish is called Bernoulli distribution so here we might have some heterogeneity). Two-point distribution can have only two values – 1 when the “success” of event occurs and 0 when not in some unit(!) of time. So it does not really get us to an answer to question 1, as in a unit of time you have only one or zero events. But we can solve that by dividing the unit of time to the smaller units (one hour to 60 minutes and then even a minute to seconds and so on…). We can use a generalization of two-point distribution, or maybe the better word for it will be an extension, which is the binomial distribution. In the end in the unit of time will be able to have a number of event occurrences. Just to recall how probability mass function of a binomial looks like:

$$x_k = k,\; p_k = P(X=k) = {n\choose k} p^k (1-p)^{n-k} \sim B(n,p)$$

Hmm, but to use it we need n – total number of events and p – the probability of success. But… we can assume that n approaches infinity and to n*p not to blow up, p needs to approach to 0, so n will be infinitely big and p will be infinitely small. Then the only parameter that we need is an expected value of a successful event. Look at below identities:

$$ P(X=k) =\lim_{n\to \infty}{n\choose k}p^k(1-p)^{n-k} = [let\; p=\frac{\lambda}{n} ]= $$ $$ = \lim_{n\to \infty}{n\choose k}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} = $$ $$ = \lim_{n\to \infty} \frac{n!}{k!(n-k)!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n}(1-\frac{\lambda}{n})^{-k} = $$ $$ = \lim_{n\to \infty} \frac{n!}{k!(n-k)!} \frac{1}{n^k} \frac{\lambda^k}{k!}e^{-\lambda} = \frac{\lambda^k}{k!}e^{-\lambda} \; \;(2)$$

And using below properties:

$$ \lim_{n\to \infty} (1-\frac{\lambda}{n})^{n} = e^{-\lambda}$$ $$ \lim_{n\to \infty} (1-\frac{\lambda}{n})^{-k} = 1 $$ $$ \lim_{n\to \infty} \frac{n!}{k!(n-k)!} \frac{1}{n^k} = \lim_{n\to \infty} \frac{n(n-1)(n-2)...(n-k+1)}{n\cdot n \cdot...\cdot n} = 1$$

We are getting to the probability mass function for a Poisson distribution:

$$ P(X=k)= \frac{\lambda^k}{k!}e^{-\lambda}$$

What might be examples of the application of Poisson distribution?

1. We might want to know what is the probability of having 1000 visitors at our website between 12:00 and 13:00 when we know that on average there are 700 visitors during that time.
2. We might want to know the probability of sell 150 pizzas on Sunday when on average we sell 120.
3. The Poisson distribution has been used as a model by insurance companies. For example, the number of freak accidents, such as falls in the shower, for a large population of people in a given time period might be modeled as a Poisson distribution, because the accidents would presumably be rare and independent (provided there was only one person in the shower).
4. The Poisson distribution has been used by traffic engineers as a model for light traffic. The number of vehicles that pass a marker on a roadway during a unit of time can be counted. If traffic is light, the individual vehicles act independently of each other. In heavy traffic, however, one vehicle’s movement may influence another’s, so the approximation might not be good.
(Credits for the last two examples belong to Mathematical Statistics and Data Analysis by John. A. Rice.)

Poisson distribution in practice

Last but not least, I would like to show you how Poisson distribution varies depending on the value of lambda. Below you will see 4 cases of different lambda values, for randomly generated samples (with n=10000 elements) from Poisson distribution. What is worth to see, that for big lambdas distribution is starting to look like a gaussian curve.

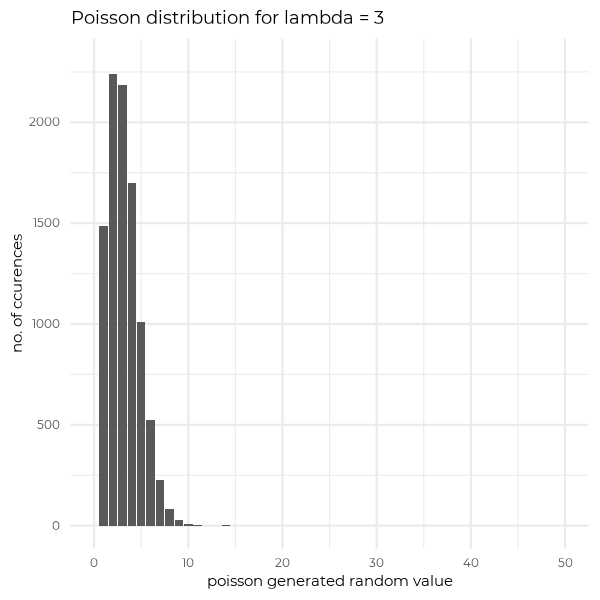
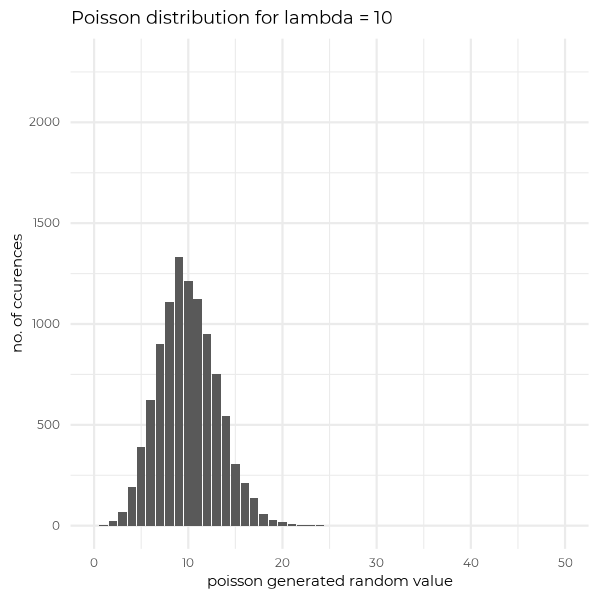
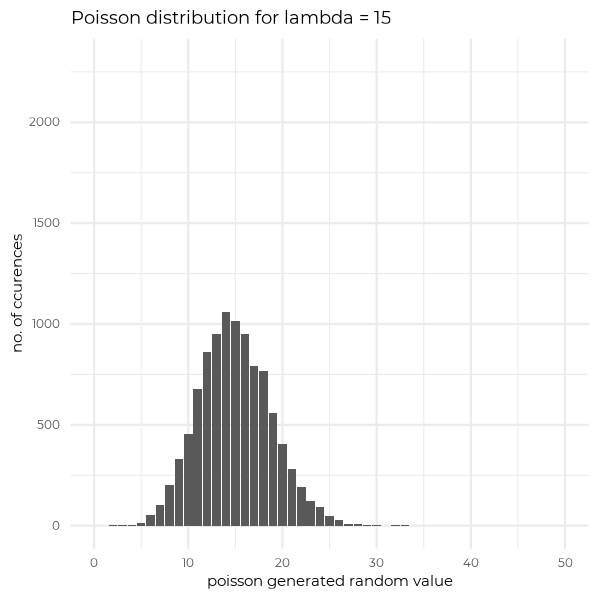
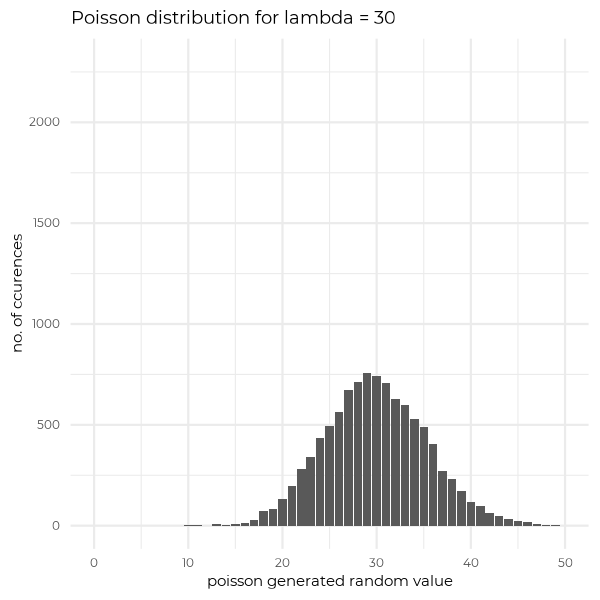
Summing up for today, Poisson distribution answers a question of the probability of k independent event occurences in a unit of time, where parameter corresponds to an expected number of event occurences in that unit of time.

Thanks for reading!

xoxo,
szarki9